Câu hỏi:
13/07/2024 11,360
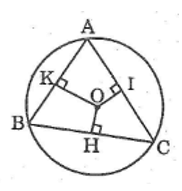
Tam giác ABC nội tiếp lối tròn trặn (O) có A > B > C. Gọi OH, OI, OK theo đuổi trật tự là khoảng cách kể từ O cho tới BC, AC, AB. So sánh những phỏng nhiều năm OH, OI, OK.
Tam giác ABC có 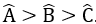
BC > AC > AB (cạnh đối lập góc to hơn thì rộng lớn hơn)
Ta đem AB, BC, AC thứu tự là những chạc cung của lối tròn trặn (O)
Mà BC > AC > AB nên suy ra:
OH < OI < OK (dây to hơn ngay sát tâm hơn)
Nhà sách VIETJACK:
🔥 Đề ganh đua HOT:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho lối tròn trặn tâm O nửa đường kính 25cm. Hai chạc AB, CD tuy vậy song cùng nhau và có tính nhiều năm theo đuổi trật tự vì thế 40cm, 48cm. Tính khoảng cách thân thích nhì chạc ấy.
Câu 2:
Cho lối tròn trặn (O) và điểm I nằm cạnh sát nhập lối tròn trặn. Chứng minh rằng chạc AB vuông góc với IO bên trên I ngắn lại từng chạc không giống trải qua I.
Câu 3:
Cho lối tròn trặn (O), chạc AB và chạc CD, AB < CD. Giao điểm K của những đường thẳng liền mạch AB, CD ở ngoài lối tròn trặn. Đường tròn trặn (O; OK) hạn chế KA và KC bên trên M và N. Chứng minh rằng KM < KN.
Câu 4:
Cho lối tròn trặn (O), nhì chạc AB, CD đều nhau và hạn chế nhau bên trên điểm I nằm cạnh sát nhập lối tròn trặn. Chứng minh rằng: OI là tia phân giác của một trong những nhì góc tạo ra vì thế nhì chạc AB, CD.
Câu 5:
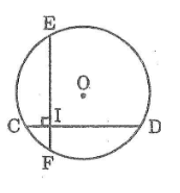
Cho hình mặt mày, nhập cơ đem nhì chạc CD, EF đều nhau và vuông góc cùng nhau bên trên I, IC = 2cm, ID = 14cm. Tính khoảng cách kể từ O cho tới từng dây
Câu 6:
Cho lối tròn trặn (O), những nửa đường kính OA, OB. Trên cung nhỏ AB lấy những điểm M và N sao cho tới AM = BN. Gọi C là giao phó điểm của những đường thẳng liền mạch AM và BN. Chứng minh rằng: OC là tia phân giác của góc AOB